
Here's a good place to take a look at comparing negative and positive exponents and seeing how they behave on a graph. Then solve as usual with the power rule.ĭefinitely not as confusing as it first looked, right? Our first step is just to flip the numerator and denominator to get rid of all the negatives in the exponents. With that in mind, let's work through the question. If you move it to the numerator, its exponent also becomes positive. The same actually works for negative exponents on the bottom.

If you ever see a negative exponent on the top of a fraction, you know that if you flip it to the bottom, it'll become positive. So moving on from the above, we can continue solving with the negative exponent as we did before.Īs you can see, the final answer we get is negative!. However, keeping the -1 outside helps us work with the negative exponent a little easier and allows us to illustrate what's happening. Multiplying in that -1 will turn the equation back into what it was originally. One way you can rewrite the question we're given is the following: Again, just move the number to the denominator of a fraction to make the exponent positive. Since d-3 on the bottom has a negative exponent, it is moved to the. In this case, we've got a negative number with a negative exponent. The top and bottom both contain negative exponents. Flip the number in the numerator into the denominator and vice versa. Then, solving for exponents is easy once we have it in a more calculation-friendly form. Solving with Negative Exponents Make the number a fraction or put it over one. We'll start with regular numbers with a negative exponent, then move on to fractions that have negative exponents on both its numerator and denominator.Īs we learned earlier, if we move the number to the denominator, it'll get rid of the negative in the exponent.

Let's try working with some negative exponent questions to see how we'll move numbers to the top or bottom of a fraction line in order to make the negative exponents positive.
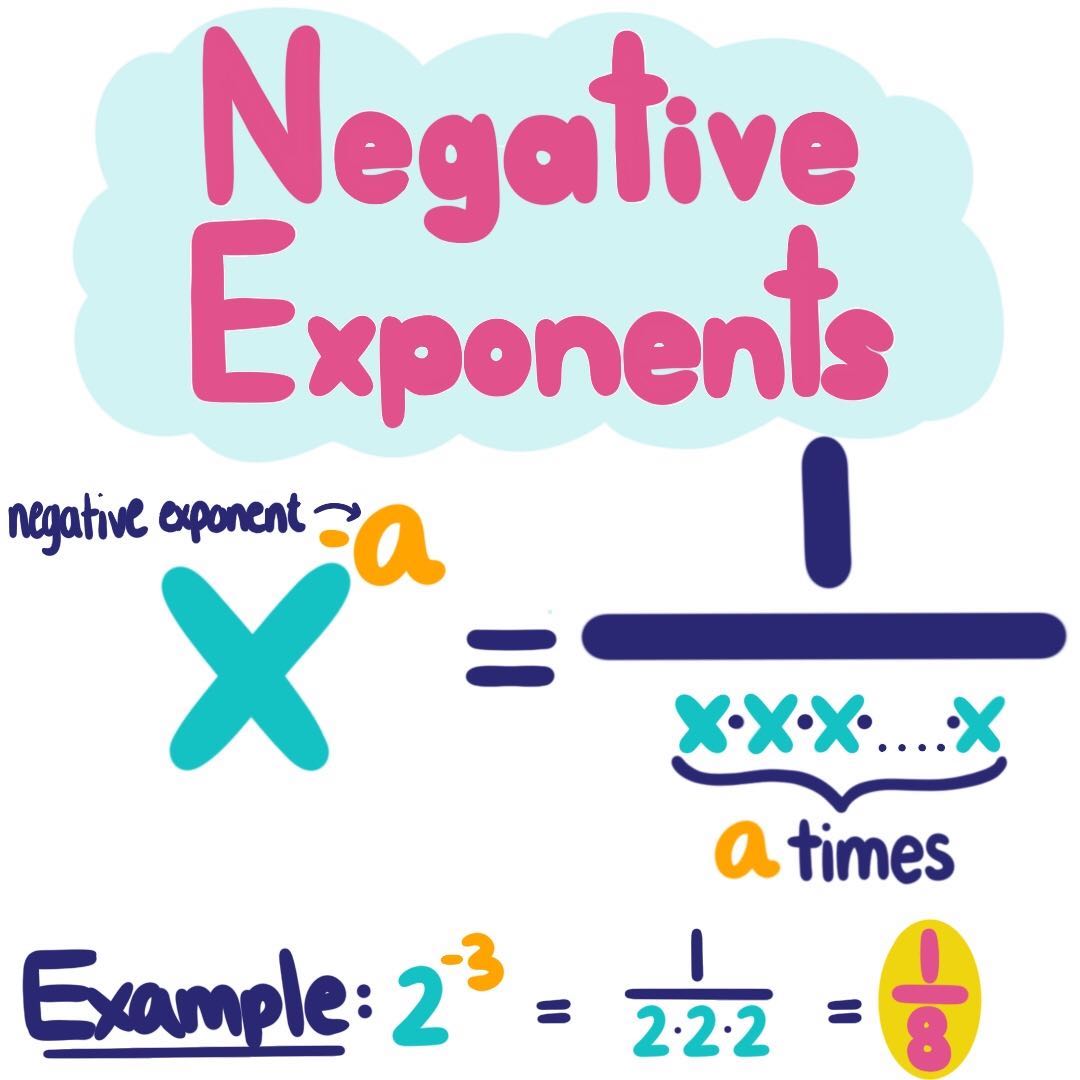
NEGATIVE EXPONENTS IN DENOMINATOR HOW TO
You'll soon understand all the basic properties of exponents! How to solve for for negative exponents There'll be a link to a chart at the end of this lesson that can show you how that relationship comes about. Learning this lesson will also help you get one step closer to understanding why any number with a 0 in its exponent equals to 1. That's the main reason why we can move the exponents around and solve the questions that are to follow. However, you can actually convert any expression into a fraction by putting 1 over the number. You might be wondering about the fraction line, since there isn't one when we just look at x^-3. For example, when you see x^-3, it actually stands for 1/x^3. In other words, the negative exponent rule tells us that a number with a negative exponent should be put to the denominator, and vice versa. In other words, negative exponents in the numerator can be written as positive exponents in the denominator, and negative exponents in the denominator can be. The worksheet topics below are arranged alphabetically because this skill falls into the dead middle of most spiral curriculums.A negative exponent helps to show that a base is on the denominator side of the fraction line. There are also plenty of practice worksheets and quizzes to help you gauge where you stand with each topic. Step One: Rewrite the Value with Negative Exponent as a Fraction Since we are performing division (the inverse of multiplication), we will rewrite the value as a fraction with a numerator of one. Each topic has an independent lesson that will teach you the skill and a guided lesson that will baby step you into to performing these calculations all on your own. To determine the denominator, we make the negative exponent positive.īelow you will find eleven topics that include exponents in some way shape and form. The fraction is made up of a numerator equal to one. This is because a fractional exponent means that the base is on the wrong side of the fraction line (the denominator). When an exponent is a negative number the result is always a fraction.

When a building or home is built the number of square feet determines the value of everything. You will find this math at all construction sites. In this way exponents are really a shorthand form of math. For example, 6 3 just indicates that we multiply 6 by itself 3 times or 6 x 6 x 6. The number of the exponent indicates how many times the base is multiplied by itself. You may also hear them referred to as indices that term creeped in during the late seventeenth century. If a negative exponent is on the top of the fraction (which means it is the numerator), then moving it to the bottom of the fraction (making it the denominator). An exponent is often referred to as a number that is raised to a certain power.


 0 kommentar(er)
0 kommentar(er)
